A Picture is Worth More Than a Thousand Words • Images & 2D Fourier Transforms in Python

For article #20 on The Python Coding Stack, I'm revisiting one of my tutorials from the pre-Substack era

Jul 22, 2023

What’s in a picture? We deal with images all the time. But let’s dive a bit further to understand what they are.

Look at this image. What do you see?

Sure, you can see a number of balconies in a terrace of houses. These balconies are a common sight in Malta, my native country.

But that's not quite what I'm asking for. So let me try again. What's this image made of? Not the stone and wood and paint in the houses and balconies. What's the image itself made of? What are the individual units that make up the image?

Pixels… is a common answer. And it's a good answer, too.

But my personal favourite is a different one: Sines and cosines.

Any image can be reconstructed using only sines and cosines. And since this is The Python Coding Stack and not The Science Stack (now, that's a good idea for another substack if I ever wanted to start another one), I'll explore this and convince you of this result using Python code and the NumPy and Matplotlib duo.

So, let me start by showing you the result. In this video, you'll see individual sines and cosines flash in front of you on the left. These are two-dimensional representations of sines and cosines. On the right, you'll see the sum of these sines and cosines. So, as the video moves on, you'll see the result of adding more of these sines and cosines on top of each other on the right-hand side:

Here are a couple of other examples. How quickly can you guess the final image as you watch the video animations?

This is the 20th article published on The Python Coding Stack since I started in April. To mark this milestone, I'm publishing a different style of article to the usual ones, and I'm revisiting the most popular article I ever wrote in the pre-Substack era.

Before Substack, I wrote articles on the blog section of The Python Coding Book website. I published this article in August 2021: How to Create Any Image Using Only Sine Functions | 2D Fourier Transform in Python.

I will not cross-post the whole article. The original article is a detailed (read 'long') discussion of the maths and physics of 2D Fourier Transforms and a step-by-step tutorial through the Python code to break down any image into its component sines and cosines and create videos like the ones you saw earlier.

Instead, I'll present a brief overview in this post and refer back to the original article for anyone wanting to dive into the detail.

The Building Blocks: Sines and Cosines in 2D

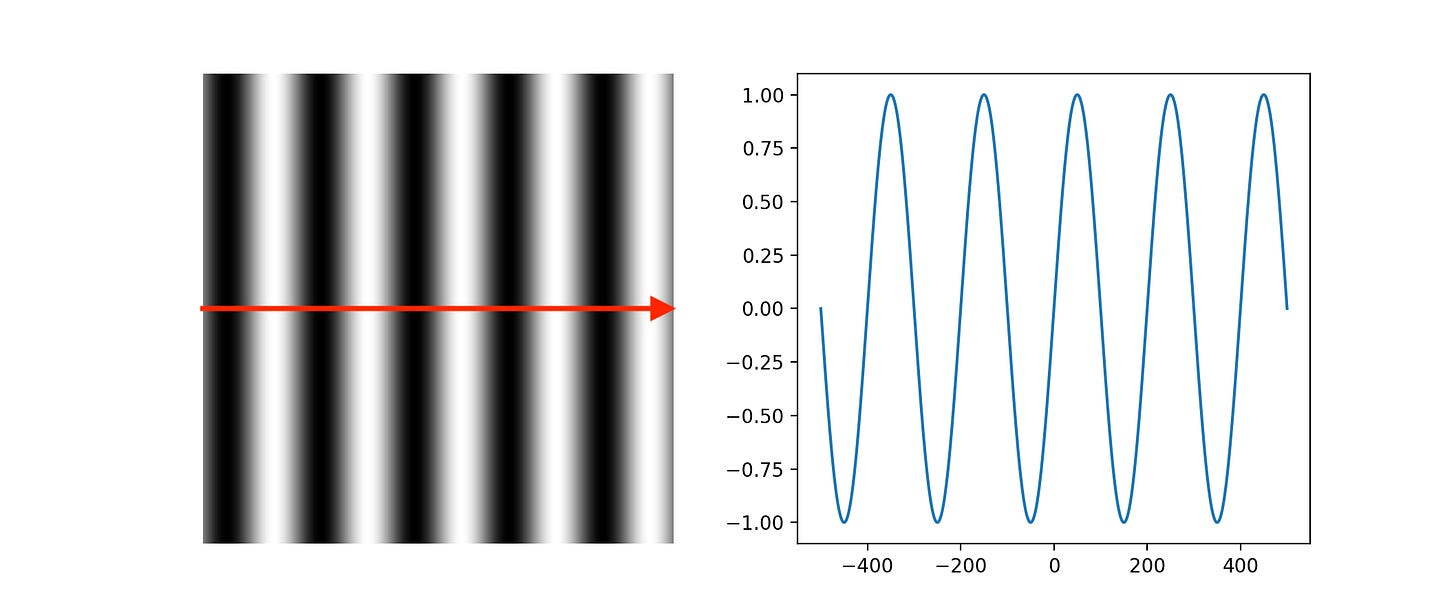
What does a sine or cosine look like in two dimensions? Here it is:

The values on a horizontal line in this image vary sinusoidally:

And we can describe the sinusoidal gratings, as these 2D sines are often called, using four properties. You can change the orientation of the gratings:

You can also change the amplitude of the peaks and troughs:

And another key parameter is how densely-packed those peaks and troughs are. This is the spatial frequency of the gratings:

There's a fourth parameter, the phase, which I'll conveniently ignore in this summary!

You can create and visualise these 2D sinusoidal gratings using NumPy and Matplotlib. All the code is in the original article.

The Star of The Show: The Fourier Transform

Let's talk about the Fourier Transform. Sounds complicated? Don't worry, we'll skip all the technical stuff here. Instead, let me show you what the 2D Fourier Transform of one of the sinusoidal gratings looks like:

And here's a couple more:

Can you spot the pattern? The dots are further apart from each other if the peaks of the sinusoidal grating are closer to each other. And their orientation matches that of the grating too. We can go further and say that these two dots have all the information needed to determine all the properties of the sinusoidal grating.

Now, add two different sinusoidal gratings to each other. These are two gratings used:

The next image shows the pattern you get when adding these two gratings together on the left and the Fourier Transform of the combined pattern on the right:

There are two pairs of dots now. Each pair represents one of the two sinusoidal gratings in the image. So the Fourier Transform can deconstruct the pattern made out of the two sinusoids into the two components.

And here, there are five different sinusoidal gratings added to each other and the Fourier Transform of the resulting pattern:

There are five pairs of dots in the Fourier Transform, although these are not always a perfect single pixel for each dot!

What's an Image? Revisited

When we summed two gratings together, we got a strange-looking pattern combining the two sinusoidal gratings used to make this pattern. When adding five gratings, the pattern was more complex as it represented the joint contributions from all five components.

So, here's the magic now. Any image is made up of lots of these gratings summed together. Every image has its unique set of gratings as building blocks. So what happens if we get the Fourier Transform of an image. Let’s use the image from the third video shown earlier with London’s Elizabeth Tower (Fun fact: Big Ben is the name of the bell inside the tower and not the tower itself):

The Fourier Transform is made up of thousands of pairs of dots. Each pair of dots contains information about the orientation, spatial frequency, amplitude, and phase of the sinusoidal grating. And if you look at each pair of dots, one at a time, you can reconstruct all the gratings that make up this image.

Final Words

A picture is worth a thousand words, yes. But it's also worth thousands of sinusoidal grating components. Possibly millions, depending on the resolution of your image, or even an infinite amount if you don't want to restrict yourself to the digital world!

I'll stop here with this short summary. But if you're interested in more detail and a step-by-step tutorial through all the steps you need to write Python code to explore this, you can read How to Create Any Image Using Only Sine Functions | 2D Fourier Transform in Python. You should also be able to google "2D Fourier Transform Python" to find this article, which is why it's quite popular!

Next up on The Python Coding Stack is article #21, and I'll get back to normal service with the following article!

Stop Stack

#20

Recently published articles on The Python Coding Stack:
- A One-Way Stream of Data • Iterators in Python (Data Structure Categories #6) Iterators • Part 6 of the Data Structure Categories Series
- Collecting Things • Python's Collections (Data Structure Categories #5) Collections • Part 5 of the Data Structure Categories Series
- And Now for the Conclusion: The Manor's Oak-Panelled Library and getitem()[Part 2]. The second in this two-part article on Python's __getitem__() special method
- The Anatomy of a for Loop. What happens behind the scenes when you run a Python for loop? How complex can it be?
- The Manor House, the Oak-Panelled Library, the Vending Machine, and Python's getitem() [Part 1]. Understanding how to use the Python special method __getitem__(). The first of a two-part article
Recently published articles on Breaking the Rules, my other substack about narrative technical writing:
- Frame It (Ep. 3). You can't replace the technical content with a story. But you can frame it within a story.
- Whizzing Through Wormholes (Ep. 2). Travelling to the other end of the universe—with the help of analogies
- Sharing Cupcakes (Ep. 1). Linking abstract concepts to a narrative • Our brain works in funny ways
- Once Upon an Article (Pilot Episode) …because Once Upon a Technical Article didn't sound right. What's this Substack about?
- Are You Ready to Break the Rules? Narrative Technical Writing: Using storytelling techniques in technical articles
Stats on the Stack
- Age: 3 months, 1 week, and 1 day old
- Number of articles: 20
- Subscribers: 741
This article is a one-way communication. But if you want a conversation, then feel free to comment below, or even better, engage in a conversation in the Substack Chat or Notes
Most articles will be published in full on the free subscription. However, a lot of effort and time goes into crafting and preparing these articles. If you enjoy the content and find it useful, and if you're in a position to do so, you can become a paid subscriber. In addition to supporting this work, you'll get access to the full archive of articles and some paid-only articles.