Clearing The Deque—Tidying My Daughter's Soft Toys • A Python Picture Story

Exploring Python's `deque` data structure through a picture story. [It's pronounced "deck"]

Today’s article takes the form of a picture story…

It was just after three o’clock. There was plenty of time left on this Sunday afternoon. It was time for Operation Teddy Tidy-Up.

We’ve given up asking grandparents, aunts, and uncles not to buy our daughter more teddies and soft toys.

Let’s fetch the boxes.

And the soft toys can start going in the boxes…

My daughter’s plan was to line up the boxes neatly next to each other and put the teddy bears in order of preference, with her favourite soft toy in the first box.

But don’t be sad for teddies[-1]. Even the least-favourite teddy is much-loved.

This is a list configuration. The boxes are in order, and they’re next to each other. You can label them from 0 to 5. If you know the location of one box, you also know where the others are.

As with all analogies, there are some limitations to the concept of items stored in boxes. A Python list doesn’t store objects. Instead, it contains references to those objects. The objects are stored elsewhere. However, this box analogy will serve us well nonetheless.

My daughter decided to give the blue teddy bear to her little cousin. So she took it out of the box.

But my daughter had a rule with her teddy-boxes. There can be no gaps. So she moved the pink octopus from the fourth box to the third…

And the green goblin in the fifth box also had to move to another box. It moved to the fourth box to fill the gap.

There was one more move. The dragon also had to move one box to the left.

The soft toys are still in the same order even though the blue bear is missing. And there are no gaps in the boxes. But my daughter had to move lots of teddies from one box to another.

Try removing the first toy in this line of boxes, and then have fun moving all the others, one bear at a time…

In a Python context, when an element is removed from a list, all the subsequent elements are shifted one position to the left to fill the gap. This process matches the analogy of the teddy bears in boxes reasonably well and is equally time-consuming.

---

The boxes were taking too much space. I had a different idea.

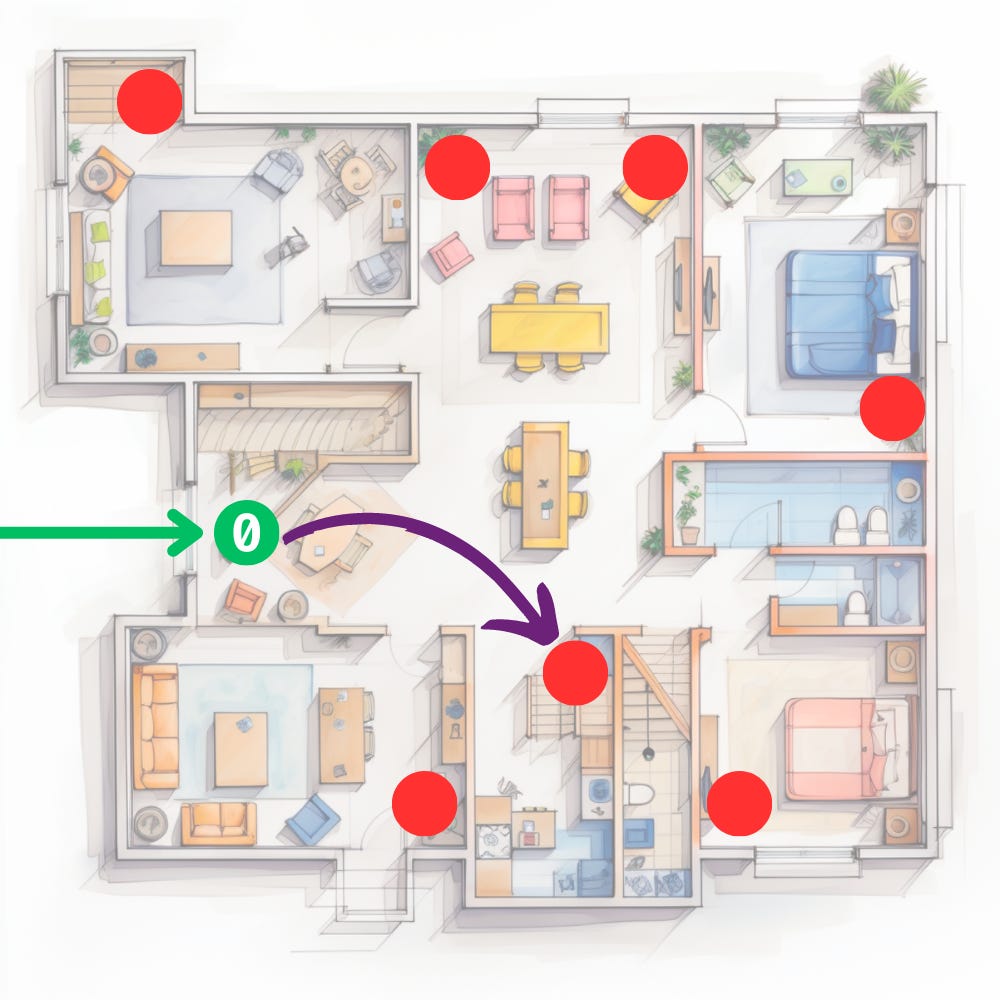
Here’s a floor plan of our home:

I placed the boxes wherever I could find some space. Each dot shows a box location.

But I had two problems. First, my memory isn’t what it used to be. Second, the order of the boxes still matters since my daughter wants the teddies in her favourite order.

I had an idea.

I could remember where one box is stored. So I remembered the first one. The one labelled 0 and shown in green.

I also added a sheet of paper in the box with the teddy.

Here’s what’s on that piece of paper:

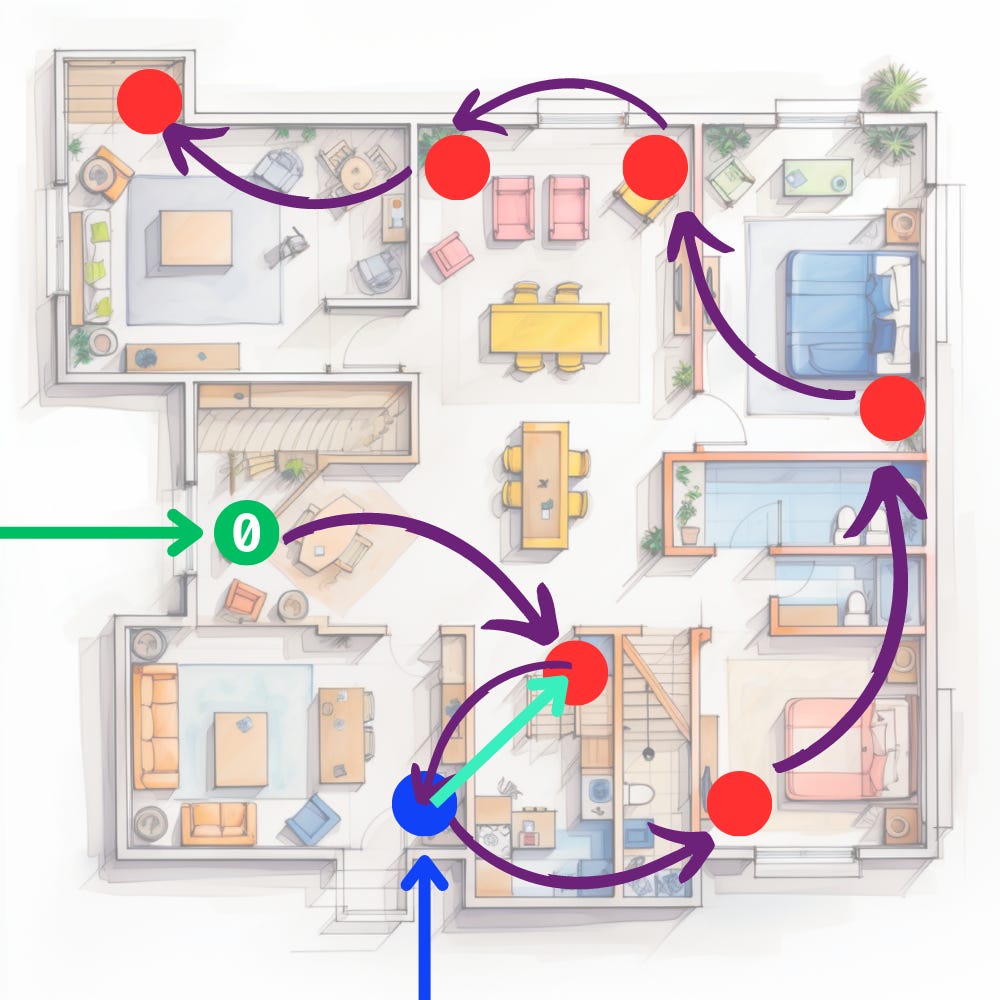
If I knew where the first box was, this sheet of paper told me where to find the second box.

So, I put a sheet of paper in the second box, too.

And now I could get from the first to the second and then to the third box.

And each box had its own sheet of paper telling where to find the next one.

Now, you may remember that my daughter gave the blue teddy bear away. This was the soft toy in the third box. I’ve marked it in blue.

She took out the teddy and gave it to her cousin. This was the sheet of paper in this box:

All I had to do was to replace the paper in the previous box with this one. The second box now had the paper saying “Next box: In the small bedroom.” I put a cyan arrow in the picture below to show you this paper’s short journey.

Nothing else changed. No teddies had to move from one box to another. Only the link between the second and third boxes changed. Here’s the new map without the blue teddy:

We removed one box and moved the paper inside it to the previous box. And that’s it. Here’s a ‘before’ and ‘after’ comparison:

This structure is a linked list. This is not the same thing as a list. The sequence of boxes all lined next to each other that you saw at the beginning of this picture story represents a list. The boxes scattered around the house with a sheet of paper showing where the next box is located represent a linked list.

The references to each element in a linked list are not next to each other, as they are in a list. But each element in a linked list has a reference to the next element in the sequence.

One application of a linked list is to create a queue. In a queue, the first item in is also the first item out. If you use a list—the sequence of boxes all lined up in a row—then each time you remove the first element in the list, you’ll have to rearrange all the other elements, just like the teddy bears in the first scenario. But if you use a linked list, all you need to do is change the reference of the first element of the sequence. The rest of the elements keep their existing positions and links.

Wait a second. I had a brainwave to make this even more efficient. I may not be able to remember where all the boxes are, but I think I can remember two of them. So I decided to remember where the last box is in addition to the first one. Here it is, also shown in green and marked with an ‘E’ for ‘End’:

I also went round the boxes to add a bit more to each piece of paper.

Each box told me where the previous box and the next box are. Now, I could go from the beginning to the end or from the end to the beginning. I could go in either direction. So I added double-sided arrows to this picture.

When the elements of a linked list reference the next and previous elements, we call it a doubly-linked list. And since a linked list can be used to create a queue, a doubly-linked list can be used for a double-ended queue…

When you need a doubly-linked list in Python, you can use the deque data structure, which is in the collections module.

---

---

A Technical Appendix

I was tempted to end this post here, at the end of the picture story. I slipped in a few Python-specific sections amid the pictures and their captions to provide context. That’s enough, I thought.

But this is still a technical article. So let me add some Python code. I’ll keep this appendix brief. I’ll re-use code I published in my first ever self-published technical article about Python (and not one published on Real Python, which predate “my own” articles.) This was in July 2021.

Empty a list and a deque from the left

Let’s create a sequence of random numbers and store the numbers in a list and a deque:

There are a million numbers. You run loops to empty the list and the deque from the left—always removing the first number in the sequence. Here’s the output I get on my system. Performance on your system may vary:

Emptying a list from the left is very expensive, not so with a deque
(time to put the kettle on...)
Time to empty list from left: 78.19841980934143
Time to empty deque from left: 0.04054713249206543

It takes well over a minute to empty the list from the left but a fraction of a second to empty the deque. Recall that the list is analogous to the row of boxes with teddy bears. If you remove the first one, you have to take each of the remaining bears and move it to the previous box. Whereas when you remove the first item from a deque, you don’t need to visit all the other boxes.

This behaviour is what’s required in a queue. The item to take out from the list is the one that’s been there the longest—the first one.

Empty a list and a deque from the right

Let’s empty the same structures from the right instead:

There’s no difference in performance in this case:

However, emptying a list from the right is not expensive
Time to empty list from right: 0.03871321678161621
Time to empty deque from right: 0.03797125816345215

When you remove the last of the teddy bears from its box, you don’t need to move any of the others.

So is a deque always better?

No.

I won’t give a long discussion, I’ll just show one example. Let’s fetch the middle element from both structures. We’ll fetch this item a million times to get a meaningful time estimate for comparison:

Here’s the output:

But, fetching an item from the middle of a deque is expensive, unlike lists
Time to fetch middle element from list 1000000 times: 0.14912009239196777
(time to drink that tea you made earlier...)
Time to fetch middle element from deque 1000000 times: 45.576027154922485

In a list, it’s easy to find the middle box in the sequence as the boxes are all lined up next to each other. In a deque, you have to start from the beginning or the end of the sequence, it doesn’t matter which end since it’s a double-ended queue, and then go from one box to the next until you find the middle one. That’s slow.

Code in this article uses Python 3.11

---

---

Stop Stack

#26

• Today's article is different from normal. I thought of presenting this topic with a picture story. Does it work? Let me know your thoughts either in the comment section on this post or in the Substack Chat. Don't worry, I won't change all my articles to picture stories! But I may use this method, sparingly, on other occasions.

• Recently published articles on The Python Coding Stack:

  • The Final Year at Hogwarts School of Codecraft and Algorithmancy (Harry Potter OOP Series #7) Year 7 at Hogwarts School of Codecraft and Algorithmancy • Class methods and static methods

  • Tap, Tap, Tap on The Tiny turtle Typewriter. A mini-post using functools.partial() and lambda functions to hack keybindings in Python's turtle module

  • Python Quirks? Party Tricks? Peculiarities Revealed… (Paid article) Three "weird" Python behaviours that aren't weird at all

  • The Mayor of Py Town's Local Experiment: A Global Disaster. Why variables within functions are local

  • Time for Something Special • Special Methods in Python Classes (Harry Potter OOP Series #6) Year 6 at Hogwarts School of Codecraft and Algorithmancy • Special Methods (aka Dunder Methods)

• Recently published articles on Breaking the Rules, my other substack about narrative technical writing:

  • The Rhythm of Your Words (Ep. 8). Can you control your audience's pace and rhythm when they read your article?

  • A Near-Perfect Picture (Ep. 7). Sampling theory for technical article-writing • Conceptual resolution

  • The Wrong Picture (Ep. 6). How I messed up • When an analogy doesn't work

  • The Broom and the Door Frame (Ep. 5). How the brain deals with stories

  • Mystery in the Manor (Ep. 4). The best story is the one narrated by the technical detail itself

• Stats on the Stack

  • Age: 4 months, 1 week, and 6 days old

  • Number of articles: 26

  • Subscribers: 923

• Each article is the result of years of experience and many hours of work. Hope you enjoy each one and find them useful. If you're in a position to do so, you can support this Substack further with a paid subscription. In addition to supporting this work, you'll get access to the full archive of articles and some paid-only articles.