The Strange Practices at The Broadcaster's Inn • Broadcasting in NumPy (A NumPy for Numpties article)
It doesn't take long in the NumPy world before you come across broadcasting.
The Broadcaster's Inn sits alone at the edge of the town. It's not a flashy place, but it's popular; perhaps because of the rumours, well-known among residents of Nump Town; perhaps because of its flawless, efficient service. Perhaps, those two reasons are linked.
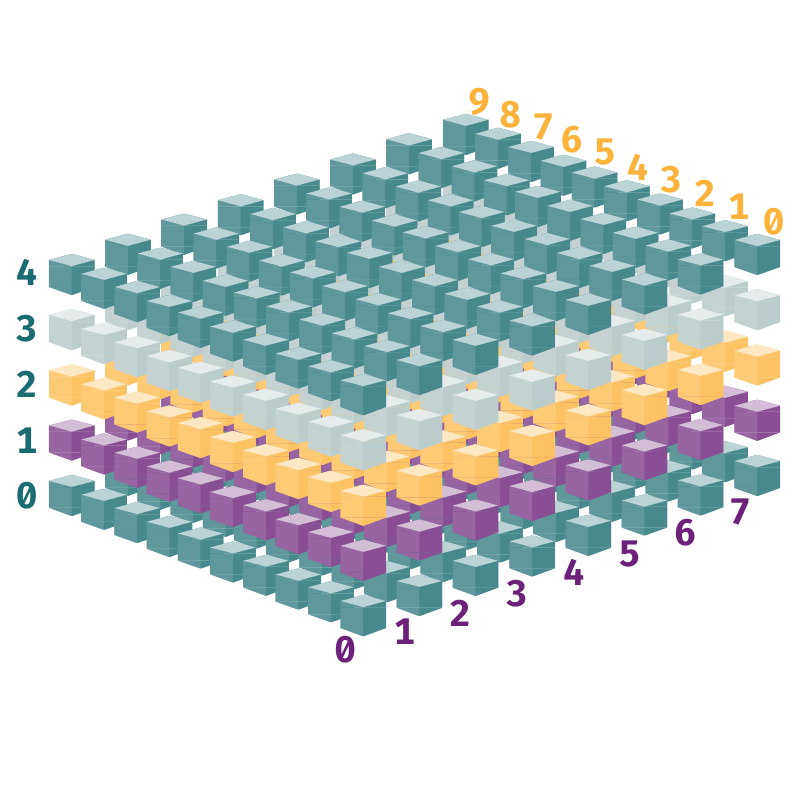
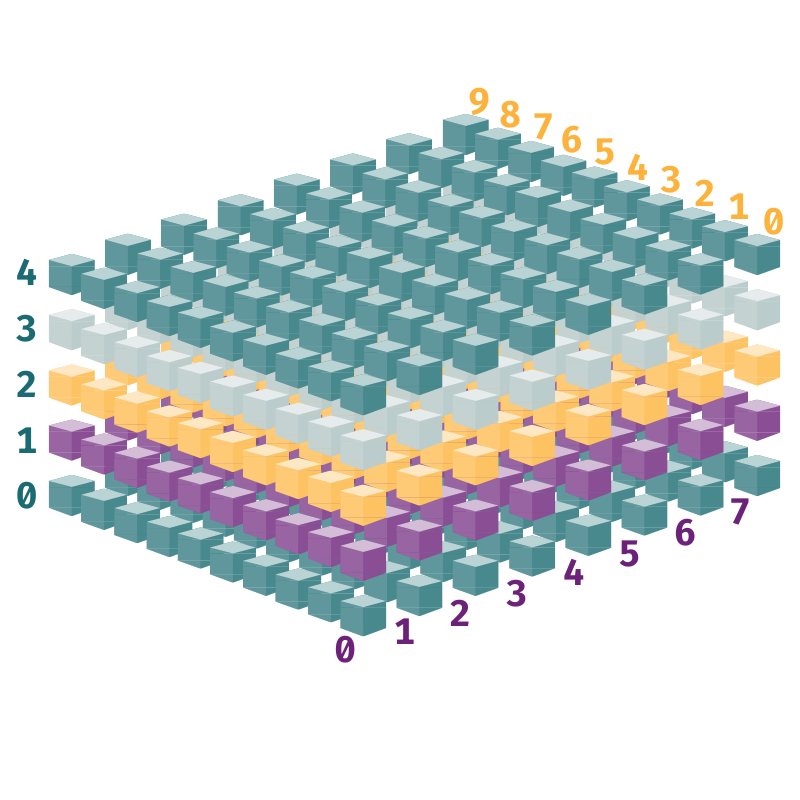
The hotel's layout is also a bit peculiar: Five identical floors, each with eight rows of ten rooms. And each room is "detached", so you can walk north to south and east to west everywhere within the grid—more weirdness to fuel the locals' stories.
Part of the mystery surrounding The Broadcaster's Inn is its staff. No one has ever met anyone who works there outside the hotel itself. Do they all come from out of town? Conspiracy theories abound.
Exclusive: I secured an interview with a staff member on condition of anonymity. Time to figure out which of the rumours are true.
The Broadcaster's Inn's Layout
The first evidence my mysterious source provided was The Broadcaster's Inn's layout. He gave me the following Python code:
He didn't tell me I needed to run the following line in the terminal first, but luckily, I knew already:
$ python -m pip install numpyOr use whatever package manager you prefer.
Here's the output of the script. I'll show it in full since I don't expect anyone to print out these articles:
[[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]]Each of the five blocks you see above represents a floor or level. Your computer can't display this array in 3D, so it deconstructs it floor by floor. In each block, each row represents one of the eight corridors. And each value in a row represents a room. There are ten rooms per corridor.
This confirms the hotel has:
5 floors
8 corridors on each floor
10 rooms in each corridor
That's 400 rooms.
Each guest is assigned a unique number when they check in. For example, when I checked in as part of my investigation—The Broadcaster's Inn didn't know I was writing a piece about them, of course—they gave me room 147. I now know what this number means. I was on the second floor*, in the fifth corridor, and the eighth room on that corridor.
It took me a while to figure it out. Then it clicked—they're using zero-indexing. I told you everything is weird about this hotel.
I can never remember which countries refer to the floor at ground level as "ground floor" and then the "first floor" is the one above, or else refer to the floor at ground level as "first floor". In any case, The Broadcaster's Inn does neither of those. The floor at ground level is the "zeroth floor."
I'll only show the output for Floor 1, which is the second floor, or the first, or whatever—the one above the floor at ground level—why's this so confusing?!
[[[ ...
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 42. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
... ]]]Note the 42 in there! I enquired why they don't add dtype=int when creating the floor plan, but my source pointed out that I shouldn't make any assumptions that guests are always assigned an integer ID. I didn't ask any further on this matter.
Since my source couldn't show me the live NumPy array with guests (we had to meet in a secret location, so we couldn't access the hotel's computer system), he generated a sample array with random numbers:
The np.random.default_rng() call creates a Generator object, which can be used to generate random numbers. I'm using a seed to get the same numbers each time I run this code. The program now creates the 5 x 8 x 10 array by calling rng.choice(). This function generates numbers between 0 and 399 without replacement to ensure each number occurs only once—otherwise, we'll get some guests mixed up, and someone else will get my room service!
Here's The Broadcaster's Inn's floor plan now. I'm only showing the zeroth floor:
[[[257 304 189 142 179 164 84 3 341 325]
[ 32 226 391 175 102 224 306 367 243 250]
[159 334 292 219 37 168 92 135 281 366]
[311 289 115 193 275 33 35 244 269 186]
[174 359 368 59 138 54 136 352 316 7]
[353 95 223 343 90 15 302 255 297 280]
[207 375 69 82 253 240 61 28 369 381]
[298 395 229 345 172 364 357 230 121 337]]
... ]]]The 11am Cleaning Routing • Broadcasting
The Broadcaster's Inn has a reputation for its room-cleaning process. All guests must be out of their rooms between 11:00am and 11:15am, and all the rooms must be cleaned in that quarter of an hour. This is one of those activities that people talk about. How does the hotel manage to clean all 400 rooms in just a quarter of an hour? This has been one of the mysteries surrounding The Broadcaster's Inn for centuries.
But my scoop reveals this mystery.
My source told me they call this process broadcasting. I guess they get this from the hotel's name. But here's where it gets weird—and this confirms some of the most outlandish rumours about The Broadcaster's Inn.
Apparently, the hotel is one of the last remaining places with an ancient form of magic, dating back to Merlin's time. Staff members can duplicate themselves for a short period of time and perform the same actions in multiple locations. But there are some rules, otherwise the magic won't work.
I couldn't understand this either when my source first explained it. So, I'll take you through the same steps he used to explain everything to me.
When a staff member cleans a room, they mark the room with a negative number in the array representing the hotel. So, if my ID number is 42, the cell representing my room changes to -42 once they clean it. Don't ask—that's what they do!
Therefore, the effect each staff member has on the room they clean is to multiply by -1. But a staff member only has time to clean one room in the 15-minute interval. Without magic, the hotel needs 400 staff members:
The array staff_cleaning is an array with the same shape as the broadcasters_inn array with values of -1 everywhere. I'll show the array in full:
[[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]
[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]
[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]
[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]
[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]]
It's 11:00am. All we need to do is multiply broadcasters_inn, which represents each room in the hotel, with staff_cleaning, which represents each staff member and their action on each room:
At 10:59 am, 400 staff members stand outside the door of a room. The staff members stand in the same geometry as the rooms: one staff member in front of each room.
It's too expensive to hire 400 staff members
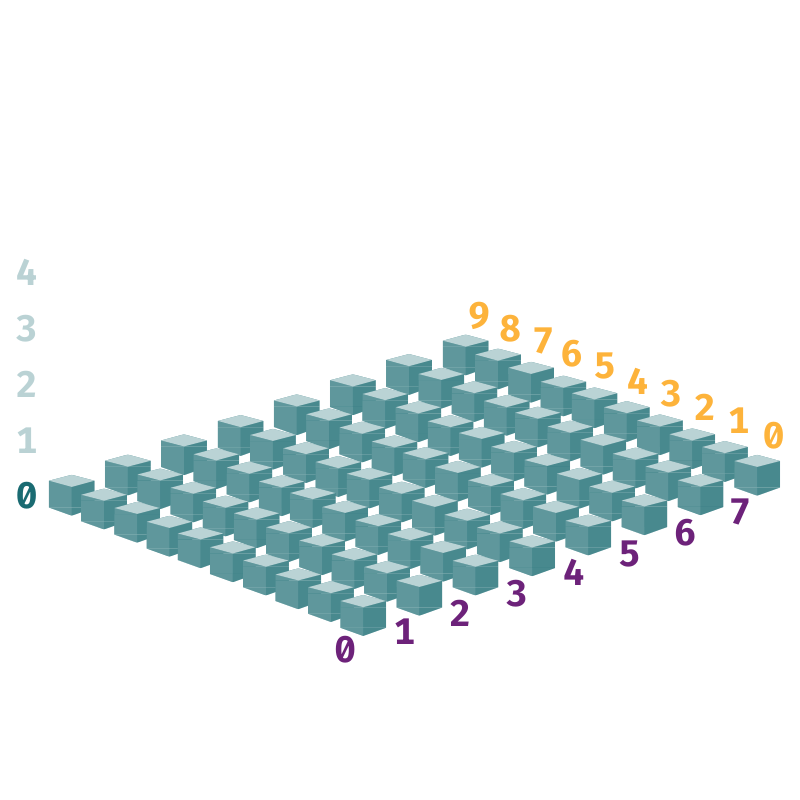
But it doesn't make sense to hire 400 staff members. It's too expensive. This is where ancient magic becomes relevant. Let's say there are 80 staff members. Recall that there are 80 rooms on each floor at The Broadcaster's Inn.
At 10:59am, they're all on the ground floor—that's the floor with index=0. Each staff member is standing in front of a room on this floor so that every room on Floor 0 has a staff member in front of it. However, none of the rooms on the other floors have staff members ready to spring into action as soon as the clock strikes 11:00am.
Here's the staff_cleaning array now:
And here's what staff_cleaning looks like:
[[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]]It's a 2D array representing one floor of the hotel. Notice how this array is identical to the first block in the 5 x 8 x 10 array we had earlier. Each row represents a corridor on Floor 0, and each value in a row represents a room. There are eight corridors and ten rooms in each corridor.
This array represents a staff member standing in front of each of these rooms:
The clock is about to strike 11:00am. Ready?
This is where the ancient magic kicks in. Each of the 80 staff members magically replicates on each floor so that there are five copies of each employee, one directly above the other. Therefore, each staff member can clean five rooms at the same time.
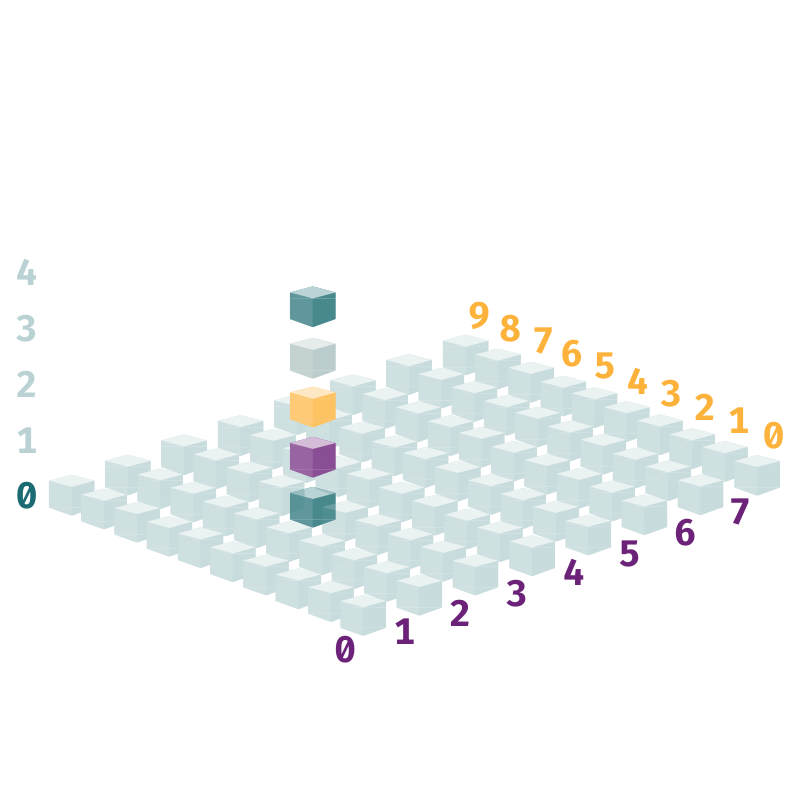
For example, the staff member outside Room 025—that's the sixth room (index=5) in the third corridor (index=2) of the bottom floor (index=0)—also magically appears in front of Rooms 125, 225, 325, and 425.
The highlighted rooms below are 025, 125, 225, 325, and 425, and they're all cleaned simultaneously by the same staff member thanks to broadcasting:
Fifteen minutes later:
[[[-257. -304. -189. -142. -179. -164. -84. -3. -341. -325.]
[ -32. -226. -391. -175. -102. -224. -306. -367. -243. -250.]
[-159. -334. -292. -219. -37. -168. -92. -135. -281. -366.]
[-311. -289. -115. -193. -275. -33. -35. -244. -269. -186.]
[-174. -359. -368. -59. -138. -54. -136. -352. -316. -7.]
[-353. -95. -223. -343. -90. -15. -302. -255. -297. -280.]
[-207. -375. -69. -82. -253. -240. -61. -28. -369. -381.]
[-298. -395. -229. -345. -172. -364. -357. -230. -121. -337.]]
[[-114. -139. -235. -388. -149. -239. -130. -221. -247. -266.]
[ -43. -52. -0. -232. -12. -147. -150. -137. -51. -312.]
[-259. -330. -373. -195. -370. -358. -300. -209. -272. -118.]
[-222. -132. -350. -318. -19. -111. -320. -16. -282. -203.]
[-171. -348. -185. -383. -328. -354. -374. -338. -198. -17.]
[-120. -301. -66. -93. -188. -27. -4. -101. -24. -346.]
[-310. -387. -109. -76. -294. -258. -210. -96. -279. -160.]
[-196. -81. -70. -295. -377. -265. -134. -144. -106. -151.]]
[[-382. -228. -38. -380. -261. -169. -291. -296. -399. -379.]
[-308. -63. -58. -317. -105. -313. -283. -284. -77. -25.]
[-215. -48. -363. -202. -200. -71. -212. -274. -344. -162.]
[-305. -98. -62. -103. -268. -26. -314. -154. -122. -238.]
[-126. -157. -117. -163. -65. -201. -49. -397. -167. -177.]
[-176. -21. -146. -220. -86. -225. -23. -181. -20. -22.]
[-331. -236. -324. -83. -1. -11. -64. -94. -217. -131.]
[-315. -57. -276. -332. -208. -42. -116. -10. -128. -246.]]
[[-191. -323. -178. -123. -340. -290. -204. -97. -199. -392.]
[-129. -148. -386. -13. -211. -329. -342. -14. -183. -347.]
[-326. -30. -119. -277. -153. -75. -41. -44. -161. -270.]
[-248. -39. -378. -85. -87. -227. -53. -40. -99. -166.]
[-293. -18. -249. -360. -333. -233. -241. -214. -287. -68.]
[ -78. -72. -155. -133. -80. -256. -285. -194. -319. -396.]
[-278. -113. -339. -125. -88. -184. -231. -267. -376. -187.]
[-237. -165. -104. -73. -145. -251. -79. -327. -91. -34.]]
[[-213. -389. -273. -254. -206. -152. -141. -263. -242. -307.]
[ -60. -393. -55. -372. -2. -140. -252. -356. -245. -36.]
[-286. -216. -385. -190. -362. -8. -355. -321. -361. -100.]
[-182. -336. -110. -234. -180. -173. -390. -107. -349. -143.]
[ -29. -335. -205. -45. -158. -47. -303. -271. -31. -264.]
[ -9. -299. -322. -74. -156. -218. -288. -262. -351. -192.]
[-112. -46. -371. -260. -6. -50. -108. -89. -67. -5.]
[-365. -56. -170. -394. -197. -384. -127. -309. -398. -124.]]]All 400 rooms have been cleaned even though there are only 80 members of staff.
It was possible to broadcast an 8 x 10 array across a 5 x 8 x 10 array. The 2D array of staff members standing in front of each room on Floor 0 was stretched into the remaining dimension—upwards.
Let's write the shapes of the arrays on top of each other:
( 8, 10 )
( 5, 8, 10 )I'll come back to why I displayed the two arrays in this format later. In NumPy, the first of these is a 2D array, and the second is a 3D array. However, this is not all that different from the following:
( 1, 8, 10 )
( 5, 8, 10 )The first array now explicitly shows that there are staff members on one floor in eight corridors in front of ten rooms in each corridor. The fact that it has one floor was implied in the 2D array (8, 10), but it is explicit in the 3D array (1, 8, 10). Yet another point we'll get back to later. Bear with me.
The first hybrid-live cohort course at The Python Coding Place starts on the 15 April. Beyond the Basics is part self-led, but with the cohort and the instructor (yours truly) keeping you on your toes, and part live, with a 90-minute live Zoom session with me every week. Plus a dedicated forum, daily exercises, office hours.
Can We Reduce Staff Members to 40?
My source told me that about 138 years ago, the hotel decided to reduce its staff from 80 to 40. Even hotels on ancient magical land need to cut costs.
The manager ordered the 40 staff members to split into groups of eight, with each group on one floor. On every floor, a staff member stood in front of the first room in each corridor. The highlighted rooms in the image below show the rooms with a staff member standing in front of them, ready to enter.
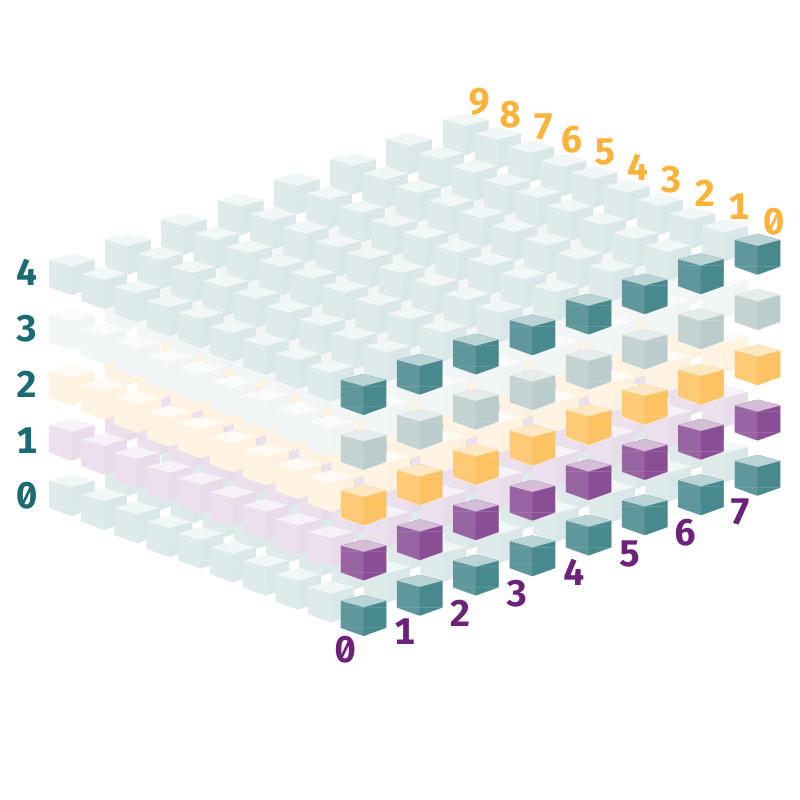
np.ones((5, 8)) and np.ones((5, 8, 1)) represent this staff configuration.For example, there was a staff member in front of Room 450—the first room (index=0) in the sixth corridor (index=5) of the top floor (index=4). But there was no one in front of the rest of the rooms in that corridor, Rooms 451 to 459.
Let's create the staff_cleaning array to represent this:
Five floors and eight corridors. Here's what the distribution of the 40 staff members looks like now:
[[-1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1.]
[-1. -1. -1. -1. -1. -1. -1. -1.]]This is not the same shape as the blocks we had earlier. The blocks from earlier represented a floor with eight corridors and ten rooms each. This array has five rows—one for each floor— and eight columns—one for each corridor.
It's almost 11:00am…
What could go wrong? But the ancient spirits didn't like this:
Traceback (most recent call last):
...
broadcasters_inn = broadcasters_inn * staff_cleaning
~~~~~~~~~~~~~~~~~^~~~~~~~~~~~~~~~
ValueError: operands could not be broadcast together with
shapes (5,8,10) (5,8) The manager hadn't studied the ancient texts well enough, and the magic of broadcasting didn't work.
Let's write the arrays one above the other again, as we did earlier when we had 80 staff members:
x Not Compatible (you'll see why later)
( 5, 8 )
( 5, 8, 10 )Or maybe you could try:
x Not Compatible (you'll see why later)
( 5, 8, )
( 5, 8, 10 )We'll see why the magic spirits don't like either of these options. Magic is fickle, it seems.
Keeping the Broadcasting Magic Spirits Happy
The manager was already trying to bring back the staff he had laid off, but he remembered something he had read in ancient texts about fooling magic spirits.
So he tried again the following day but made it clear to the magic spirits in charge of the broadcasting spells that each staff member was standing in front of one room. It's sort of obvious, but the manager was more explicit this time:
Notice the third dimension when creating staff_cleaning, even though its value is 1.
Here's how the staff members are set up now. There are still 40 of them, and they're in the same place as the previous day. But the magic spirits understand what's happening now:
[[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]
[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]
[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]
[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]
[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]]There are clearly five floors—there are five blocks of mini-arrays shown above. It's also clear there are eight corridors, just like the hotel's layout. All that's missing is the final dimension. The broadcasting magic can stretch this to cover the remaining nine rooms in each corridor by duplicating each staff member 9 times. At 11:00am, each staff member had copies of themselves magically created next to them, filling up the remaining spaces in the corridor. The staff member who was in front of Room 450 now had copies of herself in front of 451 through to 459. These are the rooms highlighted below:
And all rooms were cleaned in the 15-minute period:
[[[-257. -304. -189. -142. -179. -164. -84. -3. -341. -325.]
[ -32. -226. -391. -175. -102. -224. -306. -367. -243. -250.]
[-159. -334. -292. -219. -37. -168. -92. -135. -281. -366.]
[-311. -289. -115. -193. -275. -33. -35. -244. -269. -186.]
[-174. -359. -368. -59. -138. -54. -136. -352. -316. -7.]
[-353. -95. -223. -343. -90. -15. -302. -255. -297. -280.]
[-207. -375. -69. -82. -253. -240. -61. -28. -369. -381.]
[-298. -395. -229. -345. -172. -364. -357. -230. -121. -337.]]
...
[[-213. -389. -273. -254. -206. -152. -141. -263. -242. -307.]
[ -60. -393. -55. -372. -2. -140. -252. -356. -245. -36.]
[-286. -216. -385. -190. -362. -8. -355. -321. -361. -100.]
[-182. -336. -110. -234. -180. -173. -390. -107. -349. -143.]
[ -29. -335. -205. -45. -158. -47. -303. -271. -31. -264.]
[ -9. -299. -322. -74. -156. -218. -288. -262. -351. -192.]
[-112. -46. -371. -260. -6. -50. -108. -89. -67. -5.]
[-365. -56. -170. -394. -197. -384. -127. -309. -398. -124.]]]I'm only showing two of the five "floors", but this is the same post-cleaning 3D array you saw earlier.
It was possible to broadcast a 5 x 8 x 1 array across a 5 x 8 x 10 array. The first array was stretched along the final dimension.
Let's write the shapes of the arrays on top of each other:
( 5 8, 1 )
( 5, 8, 10 )These shapes are compatible, and the broadcasting magic works.
The Strikes of 1958
The Broadcaster's Inn has always been renowned for its efficiency. Thanks to my scoop, you're now discovering why for the first time in centuries. You're welcome!
The exception was in the summer of 1958. Eight staff members went on strike—no one knows why. Just eight. But it caused havoc. Why? Broadcasting.
The manager at the time did try. She placed eight staff members in their usual positions but only on the first four floors. The staff_cleaning array only has four "floors" now. She left the top floor empty in the hope that broadcasting does its magic, literally:
It didn't:
Traceback (most recent call last):
...
broadcasters_inn = broadcasters_inn * staff_cleaning
~~~~~~~~~~~~~~~~~^~~~~~~~~~~~~~~~
ValueError: operands could not be broadcast together with
shapes (5,8,10) (4,8,1) These array shapes are not compatible:
x Not Compatible (you'll see why soon)
( 4 8, 1 )
( 5, 8, 10 )The broadcasting magic doesn't work. The 4 x 8 x 1 array of staff members cannot be stretched both along the corridors and also up to the top floor.
By this stage of my interview with my unnamed source, I was starting to get a feel of the rules. But I wanted to make sure I fully understood them.
The Python Coding Book, First Edition, is out now in paperback or ebook
Can You Have Fewer Staff Members?
Here's what has worked so far:
When the hotel had one staff member for each room, everything worked. That's not surprising.
When the hotel filled the bottom floor with staff members but left the remaining floors empty, broadcasting stretched the array to fill the rest of the floors.
When the hotel placed a staff member at the beginning of each corridor on each floor, broadcasting stretched the array to fill the rest of the corridors.
So, I had a question for my secret interviewee:
Could you just place one person at the beginning of each corridor, but only on the bottom floor?
That's just eight members of staff. Would broadcasting stretch along the corridors and up to the rest of the floors?
My interviewee paused to think. "No one has tried this, as far as I know."
Let's try it out:
The staff_cleaning array now looks like this:
[-1. -1. -1. -1. -1. -1. -1. -1.]It represents eight staff members placed at the beginning of each corridor on Floor 0. Here are the eight rooms they're standing in front of:

np.ones(8) and np.ones((1, 8, 1)) represent this staff configuration.But…
Traceback (most recent call last):
...
broadcasters_inn = broadcasters_inn * staff_cleaning
~~~~~~~~~~~~~~~~~^~~~~~~~~~~~~~~~
ValueError: operands could not be broadcast together with
shapes (5,8,10) (8,) That was too good to be true.
Or is it?
The new staff_cleaning array doesn't look like the hotel's layout. We had this problem earlier when we first tried to make the hotel run with 40 staff members. We had to force the staff_cleaning array to be a 3D array by adding an extra dimension with a value of 1.
Would this work here, too? Maybe we need to explicitly show we're working on one floor and also that the staff members are in front of one room in the corridor they're in:
The set-up of the eight staff members now looks like this:
[[[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]
[-1.]]]The magic spirits should understand that this represents staff members standing in front of the first room in each corridor of the first floor. The format seems compatible with the hotel's shape. These values match the format for broadcasters_inn. They match the first elements of the rows of the first block of values. Let's try this out:
And…
[[[-257. -304. -189. -142. -179. -164. -84. -3. -341. -325.]
[ -32. -226. -391. -175. -102. -224. -306. -367. -243. -250.]
[-159. -334. -292. -219. -37. -168. -92. -135. -281. -366.]
[-311. -289. -115. -193. -275. -33. -35. -244. -269. -186.]
[-174. -359. -368. -59. -138. -54. -136. -352. -316. -7.]
[-353. -95. -223. -343. -90. -15. -302. -255. -297. -280.]
[-207. -375. -69. -82. -253. -240. -61. -28. -369. -381.]
[-298. -395. -229. -345. -172. -364. -357. -230. -121. -337.]]
...
[[-213. -389. -273. -254. -206. -152. -141. -263. -242. -307.]
[ -60. -393. -55. -372. -2. -140. -252. -356. -245. -36.]
[-286. -216. -385. -190. -362. -8. -355. -321. -361. -100.]
[-182. -336. -110. -234. -180. -173. -390. -107. -349. -143.]
[ -29. -335. -205. -45. -158. -47. -303. -271. -31. -264.]
[ -9. -299. -322. -74. -156. -218. -288. -262. -351. -192.]
[-112. -46. -371. -260. -6. -50. -108. -89. -67. -5.]
[-365. -56. -170. -394. -197. -384. -127. -309. -398. -124.]]]It works. I'm only showing two of the five "floors", but you'll see all five when you run this code.
Broadcasting was able to stretch in two directions:
Broadcasting stretched the staff members sideways to cover all ten rooms in each corridor.
Broadcasting stretched the staff members upwards to cover each floor in the hotel.
Could The Broadcaster's Inn run with only eight staff members? It seems the answer is 'yes'. My interviewee was concerned.
It was my turn to pause and think now. I opened my mouth to ask a question but hesitated for a short while:
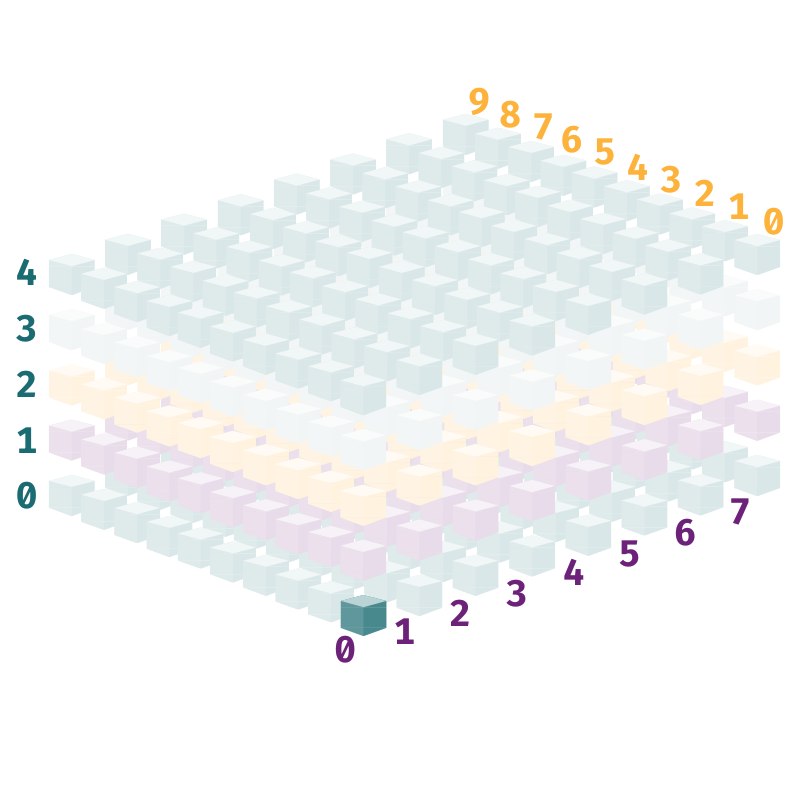
Could you also have just one person standing in front of the first room in the first corridor on the bottom floor?
I don't need to print this out for you since staff_cleaning is an integer in this scenario. It represents just one room, which is highlighted in this image:
Will this work?
[[[-257. -304. -189. -142. -179. -164. -84. -3. -341. -325.]
[ -32. -226. -391. -175. -102. -224. -306. -367. -243. -250.]
[-159. -334. -292. -219. -37. -168. -92. -135. -281. -366.]
[-311. -289. -115. -193. -275. -33. -35. -244. -269. -186.]
[-174. -359. -368. -59. -138. -54. -136. -352. -316. -7.]
[-353. -95. -223. -343. -90. -15. -302. -255. -297. -280.]
[-207. -375. -69. -82. -253. -240. -61. -28. -369. -381.]
[-298. -395. -229. -345. -172. -364. -357. -230. -121. -337.]]
...
[[-213. -389. -273. -254. -206. -152. -141. -263. -242. -307.]
[ -60. -393. -55. -372. -2. -140. -252. -356. -245. -36.]
[-286. -216. -385. -190. -362. -8. -355. -321. -361. -100.]
[-182. -336. -110. -234. -180. -173. -390. -107. -349. -143.]
[ -29. -335. -205. -45. -158. -47. -303. -271. -31. -264.]
[ -9. -299. -322. -74. -156. -218. -288. -262. -351. -192.]
[-112. -46. -371. -260. -6. -50. -108. -89. -67. -5.]
[-365. -56. -170. -394. -197. -384. -127. -309. -398. -124.]]]Yes.
I promised my concerned source I wouldn't make this article available in Nump Town so the proprietors of The Broadcaster's Inn would never find out.
The Rules of Broadcasting
Let's use what we've learnt from the rebel staff member to summarise the rules of broadcasting:
Arrays with the same shape
This is straightforward if you're comfortable with how NumPy works. Since the operation occurs element by element, you can perform it on two arrays with the same shape.
( 5, 8, 10 )
( 5, 8, 10 )Both arrays have the same number of dimensions (three), and each dimension has the same length. The tuple containing the length of each dimension of an array is its shape.
Arrays with the same number of dimensions if lengths are equal or one of them is 1
Let's consider this staff_cleaning array, which we didn't explicitly create earlier:
I'm using two methods belonging to NumPy's ndarray type. The first one, .ndim is the number of dimensions and the second one, .shape, is a tuple with the array's shape. We explicitly state that the staff members standing in front of every room of every corridor are doing so on one floor. The first dimension, with a value of 1, makes this clear.
The shapes of the staff_cleaning and broadcasters_inn arrays are compatible:
( 1, 8, 10 )
( 5, 8, 10 )They have the same number of dimensions (three)
The length of each dimension is either the same or one of them has a value of 1
The dimension with a value of 1 is stretched to match its counterpart, which has a value of 5 in this example. Note that NumPy doesn't create copies of these values. It's more efficient than this!
Arrays with different numbers of dimensions with matching right-most dimensions or dimension lengths equal to 1
Now, that's a mouthful. Let's look at the following staff_cleaning array, which you already saw earlier:
When you print out np.ones((8, 10)), you'll notice one fewer pair of square brackets compared to np.ones((1, 8, 10)) since the arrays don't have the same number of dimensions.
The arrays staff_cleaning and broadcasters_inn no longer have the same number of dimensions. To figure out whether they're compatible, write them out using a "right-aligned" format:
( 8, 10 )
( 5, 8, 10 )The trailing—right-most—dimension has a length of 10 in both arrays. The second dimension from the right also matches as it has length 8 in both arrays.
The left-most dimension in broadcasters_inn doesn't have a matching dimension in staff_cleaning. NumPy treats the missing dimension as a dimension of length 1 when broadcasting.
Therefore, this becomes equivalent to the previous example, where staff_cleaning had shape (1, 8, 10).
However, when we first tried to make the hotel work with only 40 members of staff, we used the following array:
Broadcasting didn't work in this case. When we "right-align" the array shapes, we get this:
x Not Compatible
( 5, 8 )
( 5, 8, 10 )The lengths of the dimensions don't match. Even if the missing dimension is replaced with a length of 1, the array's shape would still be (1, 5, 8), which is incompatible with (5, 8, 10).
This is why we had to explicitly add the third dimension in this case:
The arrays are now compatible:
( 5, 8, 1 )
( 5, 8, 10 )The right-most dimension has length 1 and can be stretched to match its counterpart.
But do you remember the strikes of 1958? The array shapes were the following:
x Not Compatible
( 4, 8, 1 )
( 5, 8, 10 )Two dimensions don't match. The right-most dimension is fine since one of the arrays has a length of 1. However, the first dimension—the left-most one—doesn't work as the lengths 4 and 5 are not compatible.
You can see a few more examples, including some with higher dimensions, in the official NumPy documentation page for broadcasting.
Some Useful NumPy Functions
You can test your broadcasting skills with the following three NumPy functions.
First up: np.broadcast_arrays()
You can pass NumPy arrays as arguments to this function. The function will return broadcasted arrays—versions of the arrays after any broadcasting is applied. The arrays returned are views, not copies—I'll write about views and copies in the future, so for now, I'll just state this and move on!
Here's an example:
The output arrays both have the shape (5, 8, 10), which means that one array was stretched to match the other.
Here's another example:
In this case, both arrays' shapes have changed. The shapes are compatible since the arrays have the same number of dimensions, and even though none of the lengths match, one of the lengths is 1 for each dimension. The broadcasted arrays have shape (3, 5, 7).
In fact, if you've been paying attention to the whistleblower from The Broadcaster's Inn, you'll know you can even drop the first dimension in the second array:
The output arrays have the same shape as before. When you "right-align" the original arrays' shapes, you get a compatible format:
( 3, 1, 7 )
( 5, 1 )The missing dimension is equivalent to a dimension of length 1 for broadcasting purposes. The function np.broadcast_arrays() raises a ValueError if you provide incompatible arrays:
The error tells you what the mismatch is:
Traceback (most recent call last):
...
ValueError: shape mismatch: objects cannot be broadcast to a
single shape. Mismatch is between arg 0 with
shape (3, 1, 7) and arg 1 with shape (5, 4).And you can broadcast more than two arrays if you wish:
The shapes are compatible:
( 3, 1, 7 )
( 5, 1 )
( 3, 5, 1 )Another useful function is np.broadcast_to(). Rather than adding several arrays as arguments, this function needs an array and a shape, and it broadcasts the array to the required shape, if compatible.
A 2D array with shape (8, 10) is broadcast to a compatible shape, (5, 8, 10). And you guessed it, you'll get a ValueError if the shapes aren't compatible.
And finally, if you don't care about the final arrays but you just want to figure out the shape of a broadcasted array, then you can use np.broadcast_shapes().
You can include tuples with shapes of arrays, and the function returns a tuple with the broadcasted shape:
Final Words
Broadcasting is one of those NumPy topics that's not exciting by itself—yes, I left this bombshell to the end of the article!—but that's essential to how NumPy works and the efficiency it offers through vectorisation. NumPy would be harder to use and less useful if you could only perform operations on arrays with the same shape.
And The Broadcaster's Inn wouldn't be able to service all its 400 rooms at once with only 80 or 40 staff members…or eight. Or just one!
Code in this article uses Python 3.12
Stop Stack
#56
The first hybrid cohort course starts in April: Beyond the Basics. This is included with membership of The Python Coding Place.
The Python Coding Book is out (Ebook available now, paperback in a few hours from Amazon) This is the First Edition, which follows from the "Zeroth" Edition that has been available online for a while—Just ask Google for "python book"!
If you read my articles often, and perhaps my posts on social media, too, you've heard me talk about The Python Coding Place several times. But you haven't heard me talk a lot about is Codetoday Unlimited, a platform for teenagers to learn to code in Python. The beginner levels are free so everyone can start their Python journey. If you have teenage daughters or sons, or a bit younger, too, or nephews and nieces, or neighbours' children, or any teenager you know, really, send them to Codetoday Unlimited so they can start learning Python or take their Python to the next level if they've already covered some of the basics.
Each article is the result of years of experience and many hours of work. Hope you enjoy each one and find them useful. If you're in a position to do so, you can support this Substack further with a paid subscription. In addition to supporting this work, you'll get access to the full archive of articles. Alternatively, if you become a member of The Python Coding Place, you'll get access to all articles on The Stack as part of that membership. Of course, there's plenty more at The Place, too.
Appendix: Code Blocks
Code Block #1
import numpy as np
broadcasters_inn = np.zeros((5, 8, 10))
print(broadcasters_inn)
Code Block #2
import numpy as np
broadcasters_inn = np.zeros((5, 8, 10))
broadcasters_inn[1, 4, 7] = 42
print(broadcasters_inn)
Code Block #3
import numpy as np
rng = np.random.default_rng(seed=42)
broadcasters_inn = rng.choice(
400,
size=(5, 8, 10),
replace=False,
)
print(broadcasters_inn)
Code Block #4
import numpy as np
rng = np.random.default_rng(seed=42)
broadcasters_inn = rng.choice(
400,
size=(5, 8, 10),
replace=False,
)
staff_cleaning = -1 * np.ones((5, 8, 10))
print(staff_cleaning)
Code Block #5
# ...
broadcasters_inn = broadcasters_inn * staff_cleaning
print(broadcasters_inn)
Code Block #6
# ...
staff_cleaning = -1 * np.ones((8, 10))
print(staff_cleaning)
Code Block #7
# ...
staff_cleaning = -1 * np.ones((8, 10))
broadcasters_inn = broadcasters_inn * staff_cleaning
print(broadcasters_inn)
Code Block #8
# ...
staff_cleaning = -1 * np.ones((5, 8))
print(staff_cleaning)
Code Block #9
# ...
staff_cleaning = -1 * np.ones((5, 8))
broadcasters_inn = broadcasters_inn * staff_cleaning
print(broadcasters_inn)
Code Block #10
# ...
staff_cleaning = -1 * np.ones((5, 8, 1))
print(staff_cleaning)
Code Block #11
# ...
staff_cleaning = -1 * np.ones((4, 8, 1))
Code Block #12
# ...
staff_cleaning = -1 * np.ones(8)
print(staff_cleaning)
Code Block #13
# ...
staff_cleaning = -1 * np.ones((1, 8, 1))
print(staff_cleaning)
Code Block #14
# ...
staff_cleaning = -1 * np.ones((1, 8, 1))
broadcasters_inn = broadcasters_inn * staff_cleaning
print(broadcasters_inn)
Code Block #15
# ...
staff_cleaning = -1
Code Block #16
# ...
staff_cleaning = -1 * np.ones((1, 8, 10))
print(staff_cleaning.ndim)
# Output: 3
print(staff_cleaning.shape)
# Output: (1, 8, 10)
Code Block #17
# ...
staff_cleaning = -1 * np.ones((8, 10))
print(staff_cleaning.ndim)
# Output: 2
print(staff_cleaning.shape)
# Output: (8, 10)
Code Block #18
staff_cleaning = -1 * np.ones((5, 8))
Code Block #19
staff_cleaning = -1 * np.ones((5, 8, 1))
Code Block #20
import numpy as np
new_arrays = np.broadcast_arrays(
np.ones((5, 8, 1)),
np.ones((5, 8, 10)),
)
print(new_arrays[0].shape)
# Output: (5, 8, 10)
print(new_arrays[1].shape)
# Output: (5, 8, 10)
Code Block #21
import numpy as np
new_arrays = np.broadcast_arrays(
np.ones((3, 1, 7)),
np.ones((1, 5, 1)),
)
print(new_arrays[0].shape)
# Output: (3, 5, 7)
print(new_arrays[1].shape)
# Output: (3, 5, 7)
Code Block #22
import numpy as np
new_arrays = np.broadcast_arrays(
np.ones((3, 1, 7)),
np.ones((5, 1)),
)
print(new_arrays[0].shape)
# Output: (3, 5, 7)
print(new_arrays[1].shape)
# Output: (3, 5, 7)
Code Block #23
import numpy as np
new_arrays = np.broadcast_arrays(
np.ones((3, 1, 7)),
np.ones((5, 4)),
)
print(new_arrays[0].shape)
print(new_arrays[1].shape)
Code Block #24
import numpy as np
new_arrays = np.broadcast_arrays(
np.ones((3, 1, 7)),
np.ones((5, 1)),
np.ones((3, 5, 1))
)
print(new_arrays[0].shape)
# Output: (3, 5, 7)
print(new_arrays[1].shape)
# Output: (3, 5, 7)
print(new_arrays[2].shape)
# Output: (3, 5, 7)
Code Block #25
import numpy as np
new_array = np.broadcast_to(
np.zeros((8, 10)),
shape=(5, 8, 10),
)
print(new_array.shape)
# Output: (5, 8, 10)
Code Block #26
import numpy as np
new_shape = np.broadcast_shapes(
(8, 10),
(5, 8, 10),
)
print(new_shape)
# Output: (5, 8, 10)