Where's William? How Quickly Can You Find Him? • What's a Python Hashable Object?

You can ignore reading about hashable objects for quite a bit. But eventually, it's worth having an idea of what they are.

It's Winston's first day in the office. His manager asked him to hand a letter to William. The office was one of those large spaces with lots of identical cubicles separated from each other with drab grey dividers.

Winston stood outside his manager's office, letter in one hand, thinking of the best strategy to use. Should he shout out at the top of his voice:

"WHERE'S WILLLIAAAM?"

It didn't take him long to reach a decisive answer to this question: No!

Instead, he decided to check each cubicle. He started at one end of the room, stepped inside each cubicle, checked who was sitting at the desk, and moved on if that person wasn't William.

There were 63 people in the room, and Winston took about seven seconds to visit each cubicle and check who was in it. If he's unlucky and William is in one of the last cubicles, this task could take him over seven minutes. As it happened, it took him about four minutes in this case.

Winston had plenty of letters to deliver to several colleagues that day. Sometimes, he found the right person quickly. On other occasions, he had to visit most of the cubicles before finding the intended recipient.

Day 2: Winston arrived at work on his second day and was surprised to see the office was much larger—how did they manage to make the changes overnight? Never mind. There were 173 people in this office now.

"Can you give this letter to William, please?"

Winston knew the drill. He had to go through each cubicle again. But this time, if he's unlucky and doesn't find William until the end of his search, he could spend over 20 minutes looking for William.

Day 3: More teams merged with Winston's division. The office now had 992 cubicles.

"Can you give this letter to William, please?"

It could take Winston almost two hours to find William. His manager will surely have other letters for other employees that need to be delivered.

And there's no way he'll be able to remember who sits where with 992 people.

Winston's Brainwave

Winston decided to get organised. He'd create a list—but not just any list. He was determined to be as efficient as possible to impress his manager and get promoted to a less tedious job!

He decided to convert each person's name into a number by replacing each letter with its position in the alphabet and then summing all the numbers.

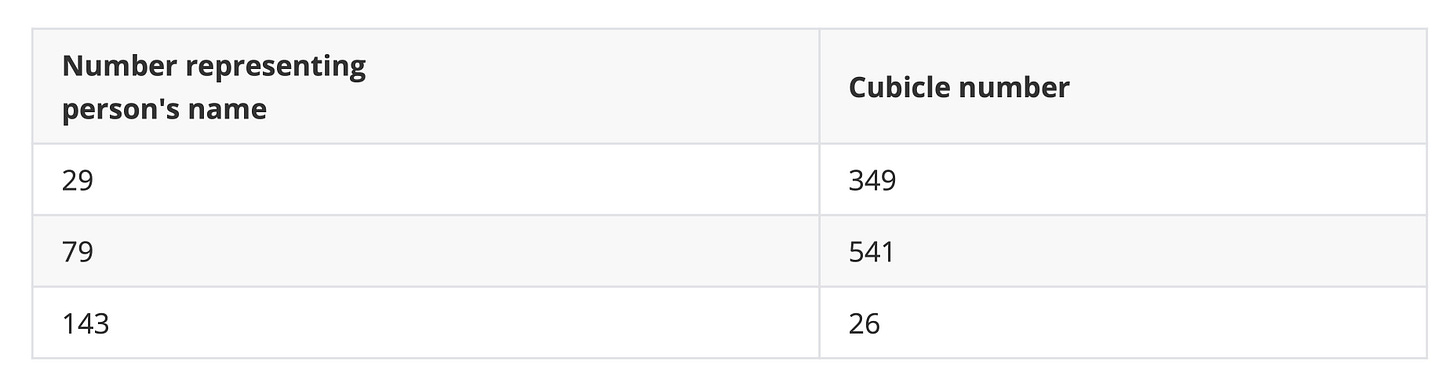
For example, Ann converts to 29:

a —>  1
n —> 14
n —> 14
total is 29

The first letter in Ann's name is "A", which is the first letter of the alphabet (I bet you knew that fact already!) The letter "n" is the fourteenth letter of the alphabet, and there are two of them. The total is 29.

William is 79. Xenophilus is 143.

Therefore, he wrote a list with these numbers in one column and the cubicle number where the employee sits in the second column. He ensured the numbers representing the person's name were in numerical order. Here's how Ann, William, and Xenophilus show up on Winston's list:

But his list contained all 992 employees and their cubicle numbers. He even wrote a short Python script to assist with converting names to numbers:

All code blocks are available in text format at the end of this article • #1

The string module contains the string ascii_lowercase with all the lowercase letters in the alphabet. The function fetches the index of each letter in a name (and adds one to deal with zero-indexing) and sums them.

"Can you give this letter to William, please?"

"Sure, I'll hand it to him right away"

Winston had a smile on his face. He quickly typed the following on his computer:

#2

And he got the following output:

79

The first column in his list is in numerical order. So it was quick for Winston to scan through the sheets of paper, look at a number, and decide whether he needed to look above or below that number. Whatever the number, he could find it quickly, homing in with his index finger. Once he found the number in the first column, his finger slid to the right to show him the cubicle number—541. He could go straight to cubicle 541 now.

Day 10: More people joined Winston's team. There are now 12,350 employees. But Winston wasn't concerned. His system could scale well. It took him nearly the same amount of time to deliver William's letter! It could have taken him up to 24 hours using the old scheme since his pace was 7 seconds per cubicle!

I’m running a series of free live workshops. Register for any of them…or all of them

Hashable Objects in Python

Dictionaries in Python aren't that different from Winston's scheme to deliver letters to his colleagues. This is the reason dictionaries are efficient at retrieving values.

We'll return to dictionaries later.

Winston prefers to use numbers rather than names in the first column of his list, as he can write them sequentially. It's much easier to find the number you're looking for. Let's say Winston's list has 100 rows on each page. If he's looking for the number 545, he can jump straight to the middle of page six!

Winston's convert_name_to_number() function is a hash function that converts the string containing the person's name to an integer. But it's not a very good hash function. We'll see some of its shortcomings throughout this article.

An object is hashable if you can create a hash value from it. You'll see later that not every data type is hashable.

Python has a built-in hash() function you can use to create a hash value—an integer—from any hashable object:

#3

Clearly, this is not quite the same as Winston's hash function!

The hash value returned by hash() doesn't change for the entire lifetime of an object. Therefore, you'll get the same hash value for "William" each time you calculate it during the execution of a program. However, the hash value can change between different Python processes. So, if you stop the program and run it again, you'll get different hash values for strings and for some other data types. And if you try to get the hash value for the names above, you'll get different values since the hash values for strings use a random seed at the start of each process.

At the simpler end of the spectrum, the hash value of an integer is the integer itself:

#4

This makes sense since an integer is already, well, an integer! No further conversion is needed.

The concept of an object being hashable is closely related to two other concepts you know about: immutability and equality. Let's explore these relationships in the following sections.

Equality and Hashable Objects

The hash value of an object represents its contents. Therefore, if two objects are equal, they must return the same hash value. Let's look at some examples:

#5

The integer 5 and the float 5.0 are not the same object. They're not even of the same type. However, they're equal. What we mean by this is that the equality operator == returns True when you compare 5 and 5.0.

You've already seen that the hash value for the integer 5 is the integer itself. The float 5.0 also returns the same hash value.

Let's consider the following tuples:

#6

You create two separate objects. The integer returned by the built-in id() function is different for both tuples, which confirms they're not the same object. Or, if you prefer, you can use the is keyword to show they're different objects.

However, these two objects are equal:

#7

You can read more about the difference between equality and identity in Understanding The Difference Between is and == in Python.

Since these two tuples are equal, they have the same hash value:

#8

Therefore, two hashable objects that are equal also have the same hash value. However, not all objects are hashable. So, equality doesn't guarantee that the objects have the same hash values–they may have no hash values at all!

Here are some examples. Let's start with a simple class that defines the .__eq__() special method:

#9

The class defines equality through the .__eq__() special method. However, the class doesn't have the special method .__hash__(). This is the special method needed to make an object hashable. Let's add it:

#10

If a class defines .__hash__(), it should also define .__eq__() since equality is relevant to the object being hashable.

Incidentally, Winston had to be careful with people having the same first name. So, he distinguishes between Jane E and Jane S, for example. Otherwise, his hash function would return the same value. The two Janes have the same name, but they work in different cubicles. They're not "equal". Therefore, Winston had to distinguish between them. Soon, he realised he was better off using first and last names for all employees to minimise the likelihood of people with the same first name.

Let's look at another example of two objects that are equal but don't have a hash value:

#11

The two lists are equal, but they're not hashable. Lists are mutable, and all built-in mutable objects aren't hashable. You'll explore this in the following sections.

Winston and the Pub Quiz

Winston had gained a reputation for his efficiency, and he was asked to organise the pub quiz for the office. He asked people to create teams of four to six people each. He then had to allocate a table for each team. He thought he'd modify his system to deal with teams instead of individuals:

#12

Winston already has the convert_name_to_number() function—this is Winston's basic hash function. So, he used it within a new function called convert_team_to_number(). This function accounts for all the names in the team.

This new function returned 333 for William's team. Winston assigned Table 1 to this team.

On the day of the quiz, Winston sat with his laptop at the entrance to check-in each team. William's team was next.

"Say your names clearly please so I can type them in!"

"William"

"Ann"

"Xenophilus"

"Zachary"

"Sarah"

And Winston tapped on his computer:

#13

And the computer said 380. Winston looked at his list. But he couldn't find 380. William explained that Sarah had joined the team at the last moment as they still had space on the team.

Hmmm! Winston had a problem. This was still William's team. It's the same team. But since its members changed (we could say that the team mutated), the "hash function" returned a different value.

The system failed him. Everyone was getting impatient as they wanted to start their evening.

Immutable and Hashable, Same Difference? [No!]

There's a close association between immutable and hashable. An object's hash value shouldn't change during its lifetime. But the object's hash value is linked to equality–equal objects have the same hash value. An immutable object ensures both those conditions are met.

Confused? Let's look at some examples. And let's start with Winston's mishap at the pub quiz. When he created William's team, he worked out the hash value using the team members' names.

The team's hash value shouldn't change, as that's the value Winston needs to identify the team in his list. However, there's no rule saying the team members can't change before the start of the quiz. So, when William turned up with an extra member on his team, the hash value changed.

That's not good. Using the team members' names to calculate the team's hash value no longer makes sense.

This is the reason you can't use built-in mutable types as dictionary keys:

#14

You can use tuples as dictionary keys but not lists. Tuples won't change during their lifetime. Therefore, their hash values won't change, either.

So, immutable types are hashable and hashable types are immutable, right?

Sort of. But in one sense, not all immutable objects are hashable. Have a look at this tuple:

#15

A tuple is immutable. But the tuple in the example above is not hashable because it contains lists within it–and lists are mutable.

And technically, you can add a .__hash__() special method to a mutable class to make it hashable. But this is rarely a good idea. Here's why.

Warning! Warning! Unsafe Code Ahead!

You decide you don't like the idea you can't use a list as a dictionary key, so you create your own version of a list:

#16

Your new class inherits from the built-in list and adds the .__hash__() special method. This class is now a hashable list:

#17

This means you can use it as a dictionary key:

#18

You create a dictionary with an instance of MyBadList as the key. This dictionary will have the other teams, too, but one team is sufficient for the purposes of this demonstration.

And you can fetch William's team table number from the dictionary:

#19

It seems like you fixed this "annoying" rule that lists can't be used as dictionary keys, after all.

But…

Recall how Sarah joined the team at the last minute. Since MyBadList is a list, you can call its .append() method:

#20

But what happens now when you try to fetch William's team's table number?

#21

This is the problem Winston encountered on the evening of the pub quiz. The team_william object hasn't changed, but its hash value has:

#22

Compare this hash value with the one you got earlier before Sarah had joined the team. They're different.

Revisiting Identity and Hash Values

You may now be wondering why you can't check for identity instead. After all, you want to know that it's the same list, right?

Wrong.

Here's an example. Let's assume you have a dictionary with grid positions as keys and a person associated with each cell in the grid. You can create this dictionary from a list of grid positions and a list of names using zip():

#23

The dictionary grid has tuples as keys. You use the tuples (0, 0), (0, 1), (1, 0), and (1, 1) to represent a 2x2 grid.

Let's get one of those grid positions at random:

#24

This works. But random_grid_position is not the same object as the key you use in the dictionary. Here's the confirmation:

#25

The tuples are equal, but they're not the same object. Therefore, we can't rely on identity to fetch a value from a dictionary. That's where the hash value comes in!

Collisions

Winston wasn't a happy man the morning after the quiz night. It was a disaster. And everyone blamed him.

He was in a bad mood. His manager asked him to deliver a letter to Roberta, a new employee. Winston tapped on his keyboard in his original script:

#26

The code outputs 79. Winston looked through his list and found that 79 is mapped to cubicle 541. He marched towards 541, head down to avoid everyone's gaze. He stepped into cubicle 541 and…

…found William sitting at his desk listening to music on his bulky headphones. He stepped out to recheck the cubicle number. He hadn't made any mistakes.

Winston went back to his computer. He decided to check his work manually:

r —> 18
o —> 15
b —>  2
e —>  5
r —> 18
t —> 20
a —>  1
​
total is 79

That's correct. So why did he end up in William's cubicle? He thought of working out William's hash value manually, too:

w —> 23
i —>  9
l —> 12
l —> 12
i —>  9
a —>  1
m —> 13
​
total is 79

Oh no! The letters in "William" and "Roberta" add up to the same value. This is a hash collision. Two separate inputs give the same hash value.

Winston's hash function is a bit too simple. Real-life hash functions use more complex algorithms, but they still can't eliminate all collisions. Behind the scenes, hash tables, such as the ones used for Python dictionaries, have mechanisms to resolve these collisions.

No, I'm not going down that rabbit hole! If you want to read more about hash functions and hash tables, have a look at this article: Build a Hash Table in Python With TDD – Real Python.

The main point I want to make is that Winston's hash function is a simplified example and doesn't represent how real hash functions work. Apart from its simplicity, it also only works on strings. Hash functions need to work on any hashable object.

The built-in hash() is good enough for most situations. However, Python also has the hashlib module that provides other implementations of hash algorithms.

Final Words

Winston wasn't having a good day. All he had to do was to swap his convert_name_to_number() function with Python's built-in hash() and ensure he used first and last names for all employees.

But why re-invent the wheel? Winston should just use a dictionary! A dictionary is Python's implementation of a hash table. Hashing is also used in sets and frozen sets.

You can survive and thrive for a long time in Python programming without worrying much about hash values. But when beginners learn about dictionaries and sets, they also learn they can't use lists and other mutable types as dictionary keys or set members. Often, they ask, "Why?" This is why.

Code in this article uses Python 3.12

---

---

Stop Stack

#61

• Thank you to all those who supported me with a one-off donation recently. This means a lot and helps me focus on writing more articles and keeping more of these articles free for everyone.

• Here's the link again for anyone who wants to make a one-off donation to support The Python Coding Stack:

• The Python Coding Book is available (Ebook and paperback). This is the First Edition, which follows from the "Zeroth" Edition that has been available online for a while—Just ask Google for "python book"!

• And if you read the book already, I'd appreciate a review on Amazon. These things matter so much for individual authors!

• And for those who want to join The Python Coding Place to access all of my video courses—past and future—join regular live sessions, and interact with me and other learners on the members-only forum, here's the link:

• Any questions? Just ask…

---

Appendix: Code Blocks

Code Block #1

import string

letters = string.ascii_lowercase

def convert_name_to_number(name):
    return sum(
        letters.index(letter) + 1 for letter in name.lower()
    )

Code Block #2

# ...
print(convert_name_to_number("William"))

Code Block #3

hash("William")
# 8064956430733888734
hash("Ann")
# -5290425712009788156
hash("Xenophilus")
# 722601165982559151

Code Block #4

hash(100)
# 100
hash(5)
# 5

Code Block #5

5 == 5.0
# True
hash(5)
# 5
hash(5.0)
# 5

Code Block #6

some_numbers = (1000, 2000, 3000)
other_numbers = (1000, 2000, 3000)
id(some_numbers)
# 4365781824
id(other_numbers)
# 4366463104
some_numbers is other_numbers
# False

Code Block #7

some_numbers == other_numbers
# True

Code Block #8

hash(some_numbers)
# 5295067188020625644
hash(other_numbers)
# 5295067188020625644
hash(some_numbers) == hash(other_numbers)
# True

Code Block #9

class SimpleTest:
    def __init__(self, data):
        self.data = data
    def __eq__(self, other):
        return self.data == other.data
first_test = SimpleTest((1000, 2000, 3000))
second_test = SimpleTest((1000, 2000, 3000))

first_test == second_test
# True

hash(first_test)
# Traceback (most recent call last):
#   ...
# TypeError: unhashable type: 'SimpleTest'

Code Block #10

class SimpleTest:
    def __init__(self, data):
        self.data = data
    def __eq__(self, other):
        return self.data == other.data
    def __hash__(self):
        return hash(self.data)
first_test = SimpleTest((1000, 2000, 3000))
second_test = SimpleTest((1000, 2000, 3000))

first_test == second_test
# True

hash(first_test)
# 5295067188020625644
hash(first_test) == hash(second_test)
# True

Code Block #11

some_numbers = [1000, 2000, 3000]
other_numbers = [1000, 2000, 3000]

some_numbers == other_numbers
# True

hash(some_numbers)
# Traceback (most recent call last):
#   ...
# TypeError: unhashable type: 'list'

Code Block #12

import string

letters = string.ascii_lowercase

def convert_name_to_number(name):
    return sum(
        letters.index(letter) + 1 for letter in name.lower()
    )

def convert_team_to_number(team):
    return sum(
        convert_name_to_number(name) for name in team
    )

print(
    convert_team_to_number(
        [
            "William",
            "Ann",
            "Xenophilus",
            "Zachary",
        ]
    ),
)

Code Block #13

# ...
print(
    convert_team_to_number(
        [
            "William",
            "Ann",
            "Xenophilus",
            "Zachary",
            "Sarah",
        ]
    ),
)

Code Block #14

# Tuples can be used as dictionary keys as they're immutable
some_dict = {(0, 0): None, (1, 2): None}

# # But lists can't as they're mutable
some_dict = {[0, 0]: None, [1, 2]: None}
# Traceback (most recent call last):
#   ...
# TypeError: unhashable type: 'list'

Code Block #15

my_tuple = ([1, 2, 3], [4, 5, 6])
hash(my_tuple)
# Traceback (most recent call last):
#   ...
# TypeError: unhashable type: 'list'

Code Block #16

# Don't do this!
class MyBadList(list):
    def __init__(self, data):
        super().__init__(data)
    def __hash__(self):
        return sum(hash(item) for item in self)

Code Block #17

team_william = MyBadList(
    [
        "William",
        "Ann",
        "Xenophilus",
        "Zachary",
    ]
)
hash(team_william)
# -5970688479492464108

Code Block #18

tables = {team_william: "Table 1"}

Code Block #19

tables[team_william]
# 'Table 1'

Code Block #20

team_william.append("Sarah")
team_william
# ['William', 'Ann', 'Xenophilus', 'Zachary', 'Sarah']

Code Block #21

tables[team_william]
# Traceback (most recent call last):
#   ...
# KeyError: ['William', 'Ann', 'Xenophilus', 'Zachary', 'Sarah']

Code Block #22

hash(team_william)
# -6447500673398513913

Code Block #23

grid_positions = [(0, 0), (0, 1), (1, 0), (1, 1)]
names = ["John", "Matt", "Jane", "Kate"]
grid = dict(zip(grid_positions, names))
grid
# {(0, 0): 'John', (0, 1): 'Matt', (1, 0): 'Jane', (1, 1): 'Kate'}

Code Block #24

import random
random_grid_position = (random.randint(0, 1), random.randint(0, 1))
random_grid_position
# (1, 0)

grid[random_grid_position]
# 'Jane'

Code Block #25

random_grid_position == grid_positions[2]
# True
random_grid_position is grid_positions[2]
# False

Code Block #26

import string

letters = string.ascii_lowercase

def convert_name_to_number(name):
    return sum(
        letters.index(letter) + 1 for letter in name.lower()
    )

print(convert_name_to_number("Roberta"))